In verification, when testing a device with random inputs, it is important to ensure that the values used span the entire operational range. This is typically accomplished by using a uniform distribution for the input stimulus, often with additional weighting on boundary values to more effectively test corner cases.
In many digital signal processing (DSP) algorithms, it is common to operate with the maximum value of a set of input signals. For this specific case, it is desirable that the distribution of the input stimuli be such that the distribution of the maximum value, measured over a window of length N, is uniform.
This article analyzes this problem and presents the implementation of a class that generates stimulus with this characteristic. Specifically, we will determine what distribution the random variable y must have in order for max(y) to follow a uniform distribution within a range of length N and then we will analyze possible implementations of this solution in Systemverilog.
1 Distribution of the random variable y
To determine which distribution f(y) makes the distribution of the maximum max(y) of N samples uniform, we start by considering the cumulative distribution function (CDF) of the maximum.
Let (Y1, Y2, ..., YN ) be a set of N independent and identically distributed random variables, and let Z be the random variable defined as Z = max(Y1, Y2, ..., YN ). In this case, it can be shown that the cumulative distribution function of Z is given by F(z) = [F(y)]N , where FY (y) is the CDF of y.1
We want the distribution of Z to be uniform on [0, 1]. This means the CDF of Z, denoted F(z), should be equal to z for 0 ≤ Z ≤ 1. Therefore, we set up the equation:
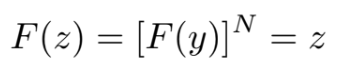
Solving for FY (y), we get:
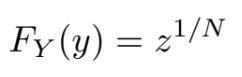
The probability density function (PDF) f(y) is the derivative of the CDF FY (y). Taking the derivative of F(y) = y 1/n, we obtain:
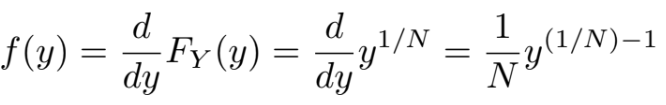
This PDF corresponds to the Beta distribution with parameters 1/N and 1, supported on the interval [0, 1].
To verify, we check that the PDF of the maximum Z is indeed uniform. The PDF of the maximum is given by:
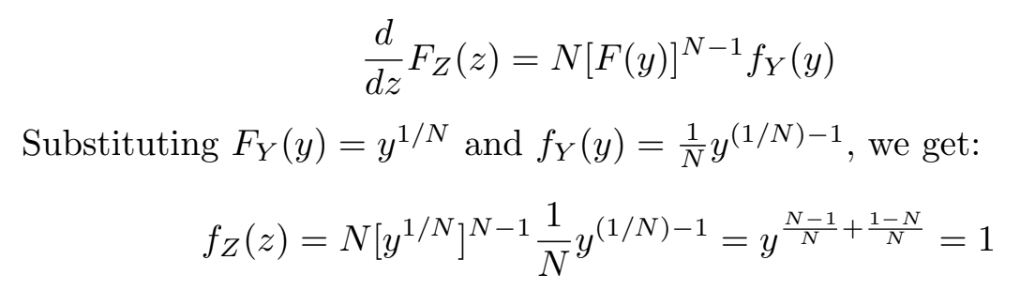
This confirms that the PDF of the maximum is uniform on [0, 1].
Thus, the distribution f(y) that makes the distribution of the maximum z uniform is the Beta distribution with parameters 1/n and 1, given by:
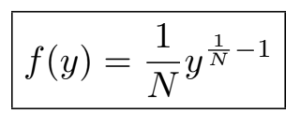
for 0 ≤ y ≤ 1.
Once we’ve demonstrated that the required distribution is the Beta distribution, the next practical challenge is how to generate variables with this distribution using standard tools.
2 How do we obtain a random variable with arbitrary distribution from a uniform random variable?
The objective is to generate a random variable y with a Beta distribution of parameters 1/N and 1. SystemVerilog provides generators for certain types of random variables—such as uniformly distributed, exponential, and normal—but does not include support for Beta distributions. Therefore, to obtain the desired distribution, it is necessary to apply known variable transformation techniques.
Let y be a random variable with an arbitrary distribution f(y), x a random variable uniformly distributed in the interval [0, 1], and g(y) = x the injective function that relates both. Under these conditions, it holds that

which gives

If we assume that g(y) = x is a function with a positive derivative, then

and from here we deduce that
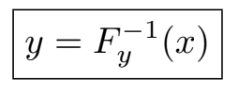
3 Systemverilog implementation for unsigned variables
The goal is to implement a class that generates a random variable y with a bit-width of REG_WIDTH, following a Beta distribution with parameters 1/N and 1. To achieve this, we begin with a uniformly distributed random variable x of bit-width X_WIDTH over the interval [0, 1].
Based on the result derived in the previous section, and considering that CDF of y is given by F(y) = y 1/N , we can express the inverse CDF as:
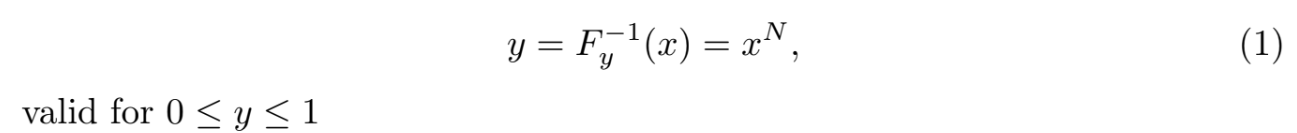
This expression yields samples with the desired distribution but restricted to the interval [0, 1]. To map these values to the full dynamic range [0, 2 REG_WIDTH−1], we introduce a scaling transformation:

with probability density function given by
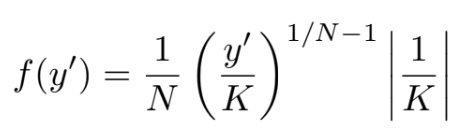
The new variable y′ retains the functional form of the original Beta distribution; however, it is not strictly a Beta-distributed variable, since its support differs from the standard interval [0, 1]. Specifically, it is defined over the interval [0, K] if K > 0, or [−K, 0] if K < 0. Nevertheless, because the shape of the distribution remains unchanged, it can be shown that the distribution of the maximum value over a sliding window of length N still follows the desired uniform distribution.
Combining equations 1 and 2, we obtain the final expression for the desired variable:

Figure 1 provides an overview of the implementation of the class d_max_uniform_unsigned. The class generates the random variable y′ by following these steps:
1. A random variable x of width X_WIDTH is created and randomized. It takes values in the interval [0, 2X_WIDTH − 1].
2. The random variable x is scaled by the factor 2X_WIDTH − 1, yielding a new variable uniformly distributed over the interval [0, 1].
3. The transformation Fy−1(x) = xN is applied, where the parameter N corresponds to WINDOW_SIZE.
4. Finally, the result is scaled by the factor K = 2REG_WIDTH − 1, producing the random variable y′, which follows a Beta distribution with parameters 1/WINDOW_SIZE and 1, and takes values in the interval [0, 2REG_WIDTH − 1].

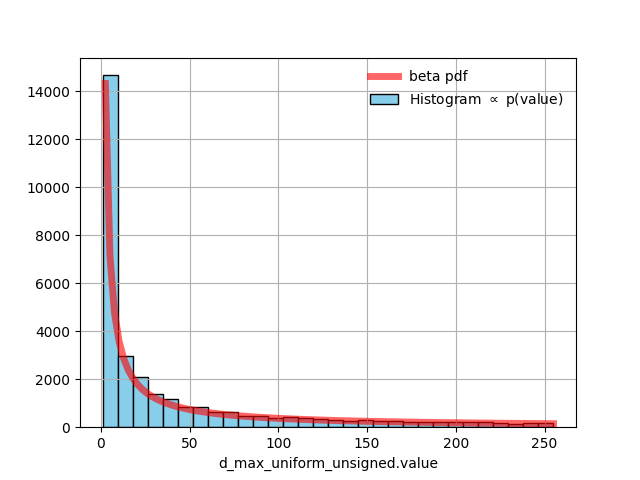
To validate the expected behavior of the d_max_uniform_unsigned class, we performed several simulations that generated multiple realizations of the random variable y′ for various values of the parameters REG_WIDTH and WINDOW_SIZE. We then plot histograms of the results and compare them with the target probability density function, a Beta distribution with parameters 1/WINDOW_SIZE and 1. As an example, the results for REG_WIDTH = 16 and WINDOW_SIZE = 2048 are shown in the following figure. It can be observed that the class appears to generate random values that respect the expected probability density function.
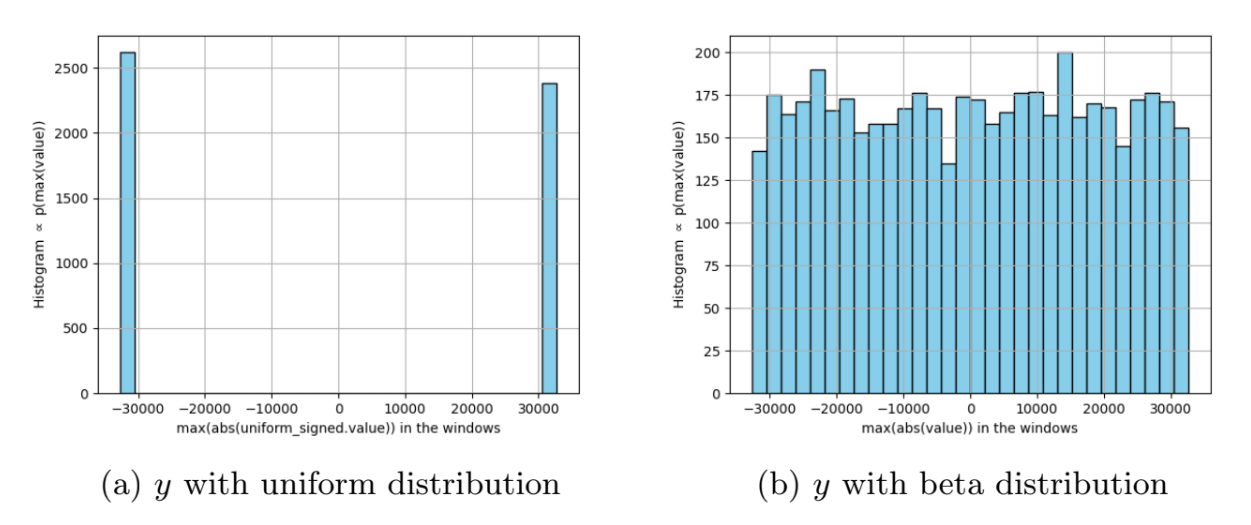
Next, we perform tests to verify that the maximum of the samples generated by the d_max_uniform_unsigned class, taken in windows of length WINDOW_SIZE, is uniform as desired. To do this, we evaluate the maximum every WINDOW_SIZE samples over the data generated in the previous test and generate histograms of the results. To assess the difference, we compare these histograms with the maximum obtained from a group of WINDOW_SIZE samples uniformly distributed in the interval [0,2REG_WIDTH]. The results are shown in the following figures. It can be observed that when uniform random variables are used, the maximum of a window of length WINDOW_SIZE tends to take values close to 2REG_WIDTH, as expected. In contrast, the maximum of a window of length WINDOW_SIZE evaluated over the sample group generated with the Beta distribution appears to have a uniform distribution in the expected range, as desired.
4 Systemverilog implementation for signed variables
Finally, we analyze the case in which the maximum is taken over the absolute value of a signed variable. This scenario can be interpreted as the superposition of two independent unsigned random variables: one defined over the interval [0, 2REG_WIDTH − 1] with a positive sign, and another defined over the interval (0, 2REG_WIDTH], which is then shifted to the interval [−2REG_WIDTH, 0). The resulting variable has a probability density function with the functional form of a Beta distribution mirrored around zero.
Based on this idea, we implement the d_max_uniform_signed class as shown in the next figure. The implementation is analogous to the unsigned case, with the main difference being that the sign of the output is selected randomly from a uniform distribution, and the generation of the variable y′ is adapted accordingly.


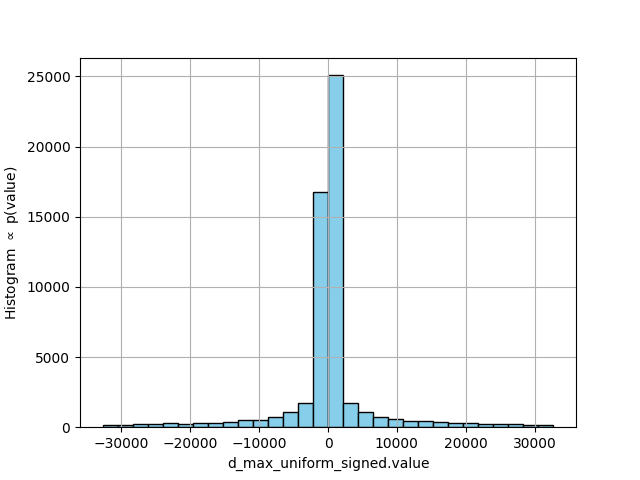
To validate the behavior of the d max uniform signed class, we perform tests analogous to those presented for the unsigned case. First, we perform a simulation, generating several samples of the random variable y′ for various values of the parameters REG_WIDTH and WINDOW_SIZE. We then plot histograms of the results and compare them with the target probability density function, a Beta distribution with parameters 1/WINDOW_SIZE and 1, mirrored around zero. The results for REG_WIDTH = 16 and WINDOW_SIZE = 2048 are shown in the following figure. It can be observed that the class appears to generate random values that respect the expected probability density function.
Next, we perform tests to verify that the maximum of the samples generated by the d_max_uniform_signed class, taken in windows of length WINDOW_SIZE, is uniform as desired. To do this, we evaluate the maximum every WINDOW_SIZE samples over the data generated in the previous test and generate histograms of
the results. To assess the difference, we compare these histograms with the maximum obtained from a group of WINDOW_SIZE samples uniformly distributed in the interval [−2REG_WIDTH, 2REG_WIDTH−1]. The results are shown in the figures below. It can be observed that when uniform random variables are used, the maximum of a window of length WINDOW_SIZE tends to take values close to 2REG_WIDTH, as expected. In contrast, the maximum of a window of length WINDOW_SIZE evaluated over the sample group generated with the Beta distribution appears to have a uniform distribution in the expected range, as desired.
5 Analysis and Improvements to the SystemVerilog Implementation
The previously presented implementation has a significant drawback: when the parameter REG_WIDTH is equal to or greater than 30, the distribution of the maximum value within the window ceases to be uniform due to numerical representation issues. Given that modern architectures often work with data widths of 32 or 64 bits, the initial implementation is not sufficient for practical use.
To avoid these issues, we propose an alternative implementation using logarithms. The desired variable, y′, can be expressed as:

By adapting this expression for its implementation in SystemVerilog, we obtain:
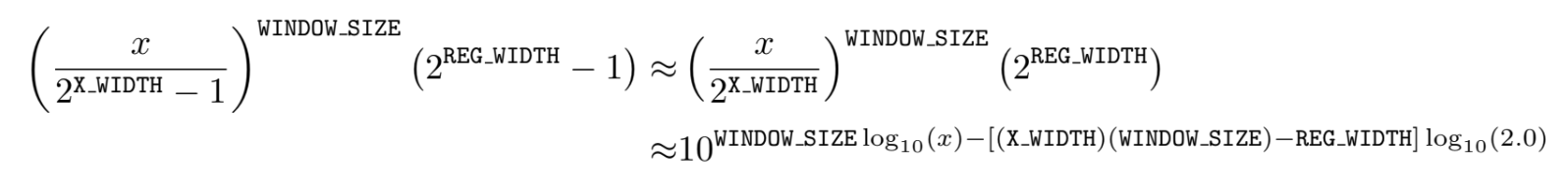
The following figure shows the resulting SystemVerilog implementation for generating unsigned samples after applying the mentioned changes.
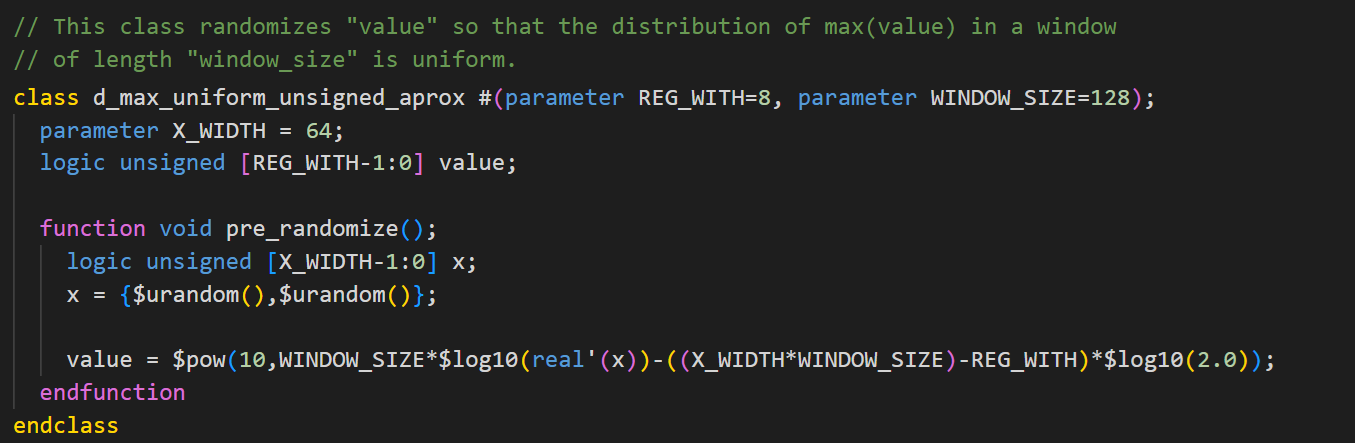
To validate the behavior of this new implementation, we created a histogram of the maximum values obtained from 5000 runs, each with a window length of WINDOW_SIZE = 2048 and an output width of REG_WIDTH = 32. The results obtained for the original implementation and the alternative implementation are presented in the figures below. In the original implementation, the numerical representation issues cause the distribution of the maximum value’s random variable to be undesirably concentrated at the extremes of the interval. In contrast, the alternative implementation produces a clearly uniform distribution of maximums, demonstrating that it has effectively solved the numerical representation problem.

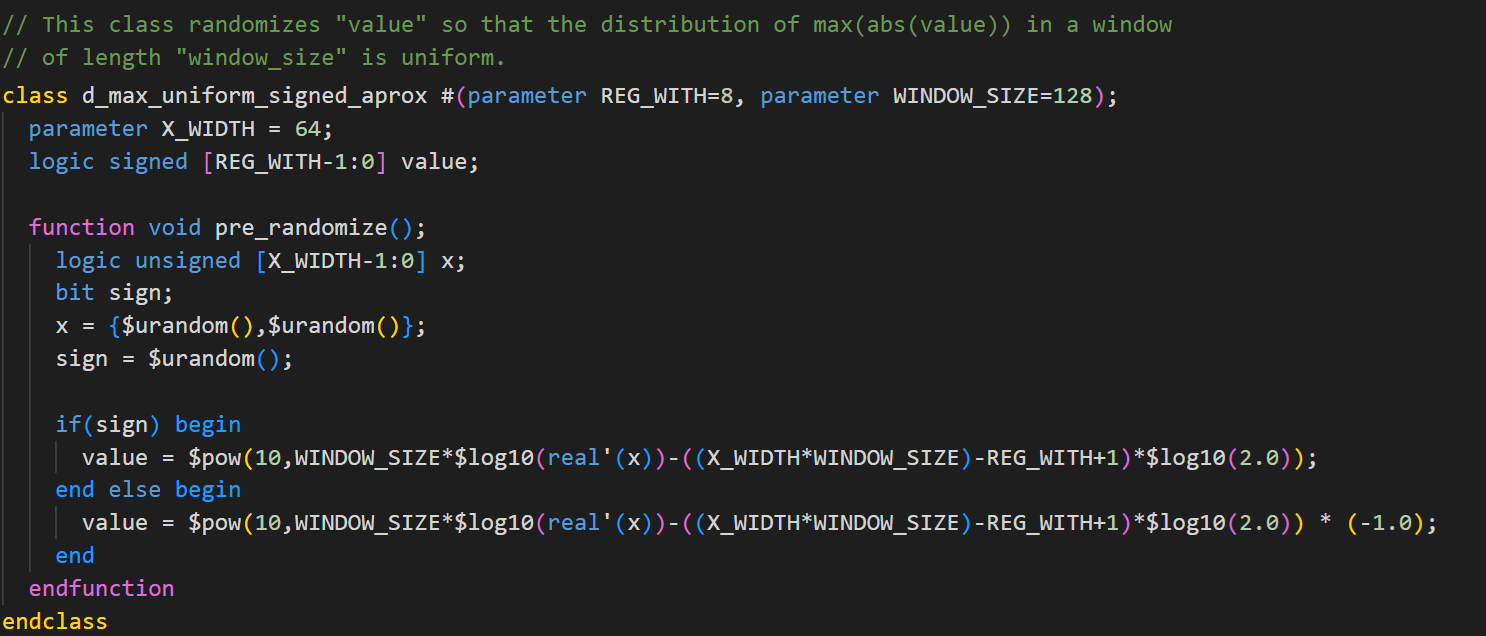
Similarly, this same technique can be applied to improve the implementation for signed variables. The following figure presents a proposed implementation for this case.
This implements the desired distribution for signed and unsigned variables and a representation range of up to at least 64 bits. This solution allows for increased coverage of the maximum value without having to perform randomizations conditioned on previous values, nor does it require randomizing all WINDOW_SIZE samples together, making it a more efficient solution in runtime.
1HSU, Hwei P. Theory and problems of probability, random variables, and random processes. New York: McGraw-hill, 1997. Chapter 4, problem 4.30
Written by Maia Desamo & Emilia Correa
If you need further information, contact us: info@emtech.com.ar